to what types of cash flows is the time value of money concept most commonly​ applied?

Capital Budgeting Decisions

65 Explain the Time Value of Coin and Calculate Nowadays and Future Values of Lump Sums and Annuities

Your female parent gives y'all $100 greenbacks for a birthday present, and says, "Spend it wisely." You want to buy the latest cellular telephone on the market but wonder if this is actually the all-time employ of your coin. You have a choice: Y'all can spend the money at present or spend it in the time to come. What should you practice? Is there a benefit to spending information technology now as opposed to saving for later utilise? Does fourth dimension have an impact on the value of your money in the time to come? Businesses are confronted with these questions and more than when deciding how to classify investment money. A major factor that affects their investment decisions is the concept of the time value of money.

Time Value of Money Fundamentals

The concept of the time value of coin asserts that the value of a dollar today is worth more than the value of a dollar in the futurity. This is typically considering a dollar today can be used now to earn more money in the future. In that location is as well, typically, the possibility of hereafter inflation, which decreases the value of a dollar over fourth dimension and could lead to a reduction in economic buying ability.

At this point, potential furnishings of aggrandizement can probably best exist demonstrated past a couple of examples. The beginning example is the Ford Mustang. The first Ford Mustang sold in 1964 for $2,368. Today's cheapest Mustang starts at a listing toll of $25,680. While a significant portion of this increment is due to additional features on newer models, much of the increase is due to the aggrandizement that occurred betwixt 1964 and 2019.

Similar aggrandizement characteristics can be demonstrated with housing prices. Subsequently World War Two, a typical pocket-sized dwelling often sold for between $16,000 and $thirty,000. Many of these same homes today are selling for hundreds of thousands of dollars. Much of the increment is due to the location of the holding, but a significant part is too attributed to inflation. The almanac aggrandizement rate for the Mustang between 1964 and 2019 was approximately 4.v%. If we assume that the abode sold for $16,500 in 1948 and the toll of the home in 2019 was most $500,000, that'southward an annual appreciation charge per unit of almost five%.

Today'south dollar is as well more valuable because in that location is less take a chance than if the dollar was in a long-term investment, which may or may not yield the expected results. On the other paw, delaying payment from an investment may be beneficial if there is an opportunity to earn interest. The longer payment is delayed, the more available earning potential there is. This can be enticing to businesses and may persuade them to take on the risk of deferment.

Businesses consider the time value of money before making an investment decision. They need to know what the time to come value is of their investment compared to today'southward present value and what potential earnings they could see considering of delayed payment. These considerations include nowadays and future values.

Before you learn most present and future values, information technology is important to examine 2 types of cash flows: lump sums and annuities.

Lump Sums and Annuities

A lump sum is a i-time payment or repayment of funds at a item betoken in time. A lump sum can exist either a present value or time to come value. For a lump sum, the present value is the value of a given amount today. For example, if you deposited $5,000 into a savings account today at a given rate of interest, say 6%, with the goal of taking it out in exactly iii years, the $5,000 today would be a present value-lump sum. Assume for simplicity's sake that the business relationship pays 6% at the finish of each year, and it also compounds involvement on the interest earned in any earlier years.

In our current instance, involvement is calculated once a year. Even so, interest tin too exist calculated in numerous ways. Some of the most mutual involvement calculations are daily, monthly, quarterly, or annually. One concept important to understand in interest calculations is that of compounding. Compounding is the process of earning interest on previous interest earned, along with the interest earned on the original investment.

Returning to our example, if $v,000 is deposited into a savings account for iii years earning six% interest compounded annually, the amount the $five,000 investment would be worth at the end of three years is $v,955.08 ($v,000 × 1.06 – $5,300 × 1.06 – $5,618 × 1.06 – $5,955.08). The $v,955.08 is the future value of $five,000 invested for 3 years at 6%. More formally, future value is the amount to which either a unmarried investment or a series of investments will abound over a specified time at a given interest rate or rates. The initial $v,000 investment is the present value. Once more, more formally, present value is the current value of a unmarried hereafter investment or a series of investments for a specified fourth dimension at a given involvement rate or rates. Another mode to phrase this is to say the $v,000 is the present value of $5,955.08 when the initial amount was invested at 6% for three years. The interest earned over the three-year period would be $955.08, and the remaining $5,000 would be the original deposit of $5,000.

As shown in the example the future value of a lump sum is the value of the given investment at some point in the future. It is also possible to accept a series of payments that found a series of lump sums. Presume that a business receives the following four cash flows. They constitute a series of lump sums considering they are non all the same amount.

The company would be receiving a stream of four cash flows that are all lump sums. In some situations, the greenbacks flows that occur each time catamenia are the same amount; in other words, the cash flows are even each flow. These types of even cash flows occurring at even intervals, such as once a year, are known as an annuity. The following figure shows an annuity that consists of 4 payments of $12,000 made at the end of each of iv years.

The nature of cash flows—single sum cash flows, even series of greenbacks flows, or uneven series of cash flows—have different effects on compounding.

Compounding

Compounding can exist applied in many types of financial transactions, such as funding a retirement business relationship or higher savings account. Assume that an private invests $10,000 in a four-year document of deposit account that pays 10% involvement at the end of each year (in this case 12/31). Any interest earned during the year will be retained until the end of the iv-year period and volition also earn x% interest annually.

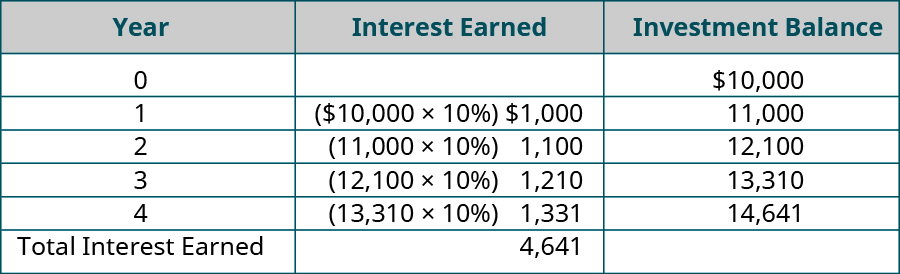
Through the furnishings of compounding—earning interest on interest—the investor earned $four,641 in interest from the iv-twelvemonth investment. If the investor had removed the interest earned instead of reinvesting it in the account, the investor would have earned $1,000 a year for four years, or $4,000 interest ($10,000 × ten% = $one,000 per year × 4 years = $4,000 total interest). Compounding is a concept that is used to determine hereafter value (more detailed calculations of future value will exist covered later in this section). But what most present value? Does compounding play a function in determining present value? The term applied to finding present value is called discounting.

Discounting

Discounting is the procedure used to calculate the nowadays value of an individual payment or a series of payments that will be received in the time to come based on an assumed interest rate or return on investment. Allow'due south expect at a elementary example to explicate the concept of discounting.

Assume that you want to accrue sufficient funds to buy a new machine and that you volition need $5,000 in three years. As well, assume that your invested funds volition earn eight% a year for the three years, and you reinvest any interest earned during the three-year period. If you wanted to have out adequate funds from your savings business relationship to fund the 3-twelvemonth investment, you would demand to invest $3,969.16 today and invest information technology in the business relationship earning 8% for three years. Afterward three years, the $3,969.16 would earn $i,030.84 and grow to exactly the $five,000 that you will demand. This is an example of discounting. Discounting is the method by which we have a futurity value and determine its current, or nowadays, value. An agreement of future value applications and calculations volition aid in the understanding of present value uses and calculations.

Future Value

There are benefits to investing money at present in hopes of a larger return in the future. These future earnings are possible because of interest payments received as an incentive for tying up coin long-term. Knowing what these future earnings will be can help a business concern determine if the electric current investment is worth the long-term potential. Retrieve, the future value (FV) as the value of an investment afterward a certain menstruation of time. Future value considers the initial amount invested, the time period of earnings, and the earnings interest rate in the calculation. For example, a depository financial institution would consider the time to come value of a loan based on whether a long-time client meets a certain interest rate render when determining whether to approve the loan.

To determine future value, the bank would need some means to determine the future value of the loan. The depository financial institution could utilize formulas, future value tables, a financial figurer, or a spreadsheet application. The same is true for present value calculations. Due to the variety of calculators and spreadsheet applications, we will nowadays the determination of both present and future values using tables. In many higher courses today, these tables are used primarily because they are relatively uncomplicated to sympathise while demonstrating the material. For those who prefer formulas, the different formulas used to create each table are printed at the top of the corresponding table. In many finance classes, you volition learn how to utilise the formulas. Regarding the utilize of a fiscal estimator, while all are similar, the user manual or a quick internet search will provide specific directions for each financial calculator. As for a spreadsheet awarding such as Microsoft Excel, there are some common formulas, shown in (Figure). In addition, Appendix C provides links to videos and tutorials on using specific aspects of Excel, such equally future and present value techniques.

Excel Formulas
Time Value Component	Excel Formula Shorthand	Excel Formula Detailed
Present Value Unmarried Sum	=PV	=PV(Rate, North, Payment, FV)
Futurity Value Single Sum	+FV	=FV(Rate, North, Payment, PV)
Nowadays Value Annuity	=PV	=PV(Charge per unit, N, Payment, FV, Type)
Futurity Value Annuity	=FV	=FV(Rate, N, Payment, PV, Type)
Net Present Value	=NPV	=NPV(Rate, CF2, CF3, CF4) + CF1
Internal Rate of Return	=IRR	=IRR(Invest, CF1, CF2, CF3)
Rate = annual interest rate
N = number of periods
Payment = annual payment corporeality, entered as a negative number, use 0 when computing both present value of a unmarried sum and future value of a single sum
FV = time to come value
PV = current or present value
Type = 0 for regular annuity, 1 for annuity due
CF = cash menstruum for a flow, thus CF1 – greenbacks flow period 1, CF2 – cash period menses 2, etc.
Invest = initial investment entered as a negative number

Since we will exist using the tables in the examples in the trunk of the affiliate, it is important to know there are four possible table, each used under specific conditions ((Figure).

Fourth dimension Value of Money Tables
Situation	Tabular array Heading
Future Value – Lump Sum	Future Value of $i
Futurity Value – Annuity (even payment stream)	Future Value of an Annuity
Nowadays Value – Lump Sum	Present Value of $1
Present Value – Annuity (even payment stream)	Present Value of an Annuity

In the prior situation, the bank would use either the Future Value of $1 table or Time to come Value of an Ordinary Annuity table, samples of which are provided in Appendix B. To use the right table, the bank needs to determine whether the client will pay them dorsum at the end of the loan term or periodically throughout the term of the loan. The Future Value of $1 table is used if the customer volition pay dorsum at the end of the period; if the payments volition be made periodically throughout the term of the loan, they volition utilize the Future Value of an Annuity table. Choosing the correct table to utilize is critical for accurate decision of the time to come value. The application in other business organisation matters is the aforementioned: a business needs to besides consider if they are making an investment with a repayment in one lump sum or in an annuity construction earlier choosing a table and making the calculation. In the tables, the columns bear witness interest rates (i) and the rows testify periods (n). The interest columns represent the anticipated involvement rate payout for that investment. Interest rates can be based on experience, industry standards, federal financial policy expectations, and risk investment. Periods represent the number of years until payment is received. The intersection of the expected payout years and the involvement rate is a number called a future value cistron. The hereafter value factor is multiplied by the initial investment cost to produce the hereafter value of the expected cash flows (or investment render).

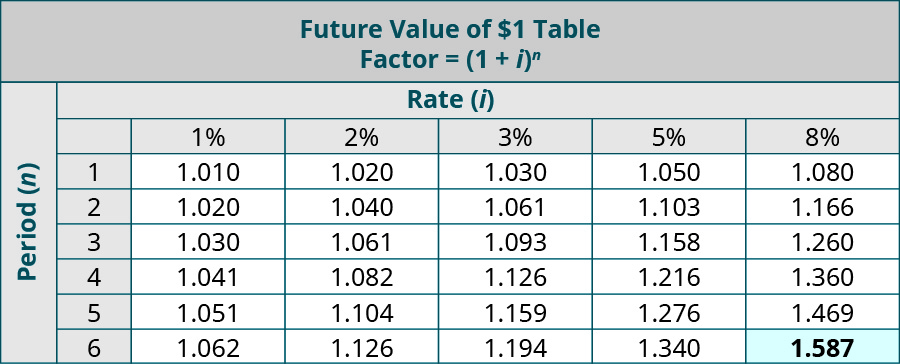
Future Value of $one

A lump sum payment is the present value of an investment when the return volition occur at the end of the period in one installment. To determine this return, the Time to come Value of $i table is used.

For example, you lot are saving for a vacation you plan to take in 6 years and want to know how much your initial savings volition yield in the future. You make up one's mind to place $4,500 in an investment business relationship at present that yields an anticipated annual return of 8%. Looking at the FV tabular array, n = 6 years, and i = 8%, which return a future value factor of 1.587. Multiplying this factor by the initial investment corporeality of $4,500 produces $7,141.fifty. This means your initial savings of $four,500 will be worth approximately $seven,141.fifty in 6 years.

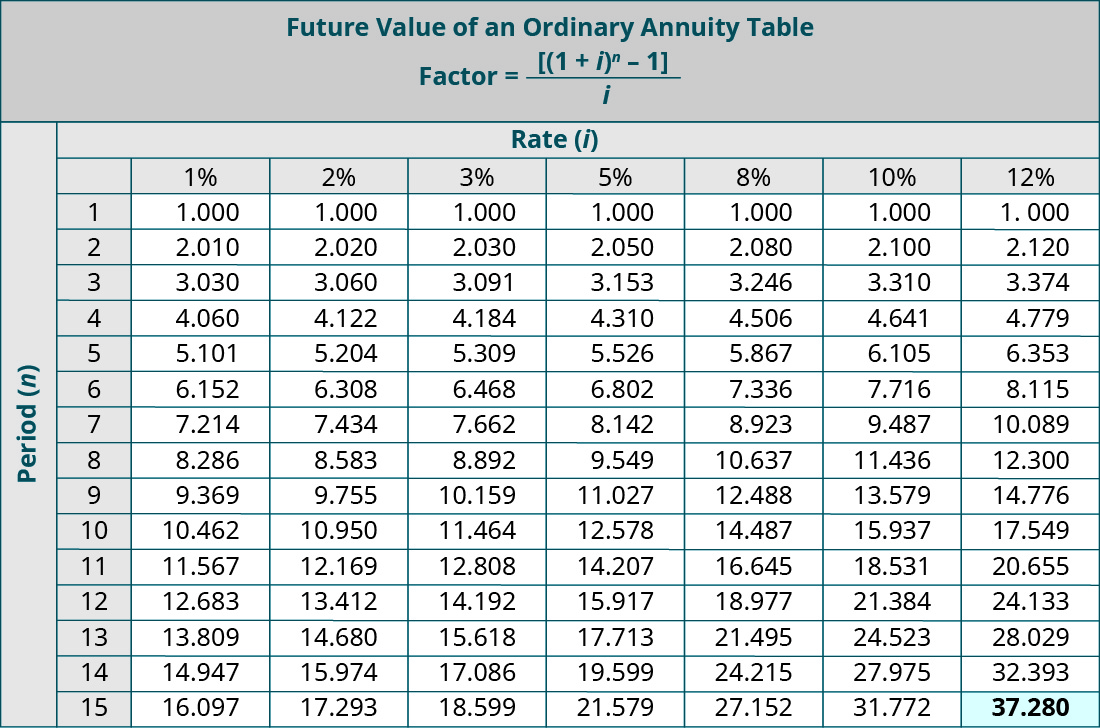
Hereafter Value of an Ordinary Annuity

An ordinary annuity is one in which the payments are made at the end of each menses in equal installments. A future value ordinary annuity looks at the value of the current investment in the future, if periodic payments were made throughout the life of the series.

For case, you are saving for retirement and wait to contribute $10,000 per year for the adjacent 15 years to a 401(k) retirement program. The plan anticipates a periodic interest yield of 12%. How much would your investment be worth in the future meeting these criteria? In this case, yous would use the Future Value of an Ordinary Annuity table. The relevant factor where north = 15 and i = 12% is 37.280. Multiplying the factor by the amount of the cash flow yields a futurity value of these installment savings of (37.280 × $x,000) $372,800. Therefore, you lot could expect your investment to be worth $372,800 at the end of 15 years, given the parameters.

Let's at present examine how nowadays value differs from future value in use and computation.

Determining Future Value

Determine the time to come value for each of the following situations. Use the future value tables provided in Appendix B when needed, and round answers to the nearest cent where required.

1. You are saving for a car and y'all put away $v,000 in a savings account. You want to know how much your initial savings will be worth in seven years if you have an anticipated annual interest rate of 5%.
2. You are saving for retirement and make contributions of $11,500 per twelvemonth for the next 14 years to your 403(b) retirement program. The interest rate yield is 8%.

Solution

A. Use FV of $1 tabular array. Futurity value gene where northward = 7 and i = five is i.407. ane.407 × five,000 = $vii,035. B. Employ FV of an ordinary annuity table. Time to come value factor where n = 14 and i = 8 is 24.215. 24.215 × 11,500 = $278,472.50.

Present Value

It is impossible to compare the value or potential purchasing power of the future dollar to today'southward dollar; they exist in dissimilar times and have different values. Present value (PV) considers the futurity value of an investment expressed in today'due south value. This allows a company to come across if the investment'southward initial cost is more or less than the future return. For case, a bank might consider the nowadays value of giving a customer a loan before extending funds to ensure that the risk and the interest earned are worth the initial outlay of cash.

Similar to the Hereafter Value tables, the columns testify interest rates (i) and the rows bear witness periods (n) in the Present Value tables. Periods stand for how oft interest is compounded (paid); that is, periods could represent days, weeks, months, quarters, years, or any interest time catamenia. For our examples and assessments, the menses (north) will nigh always be in years. The intersection of the expected payout years (n) and the interest rate (i) is a number chosen a present value factor. The present value gene is multiplied by the initial investment cost to produce the present value of the expected cash flows (or investment return).

The two tables provided in Appendix B for present value are the Present Value of $1 and the Nowadays Value of an Ordinary Annuity. Equally with the future value tables, choosing the correct tabular array to use is disquisitional for accurate determination of the present value.

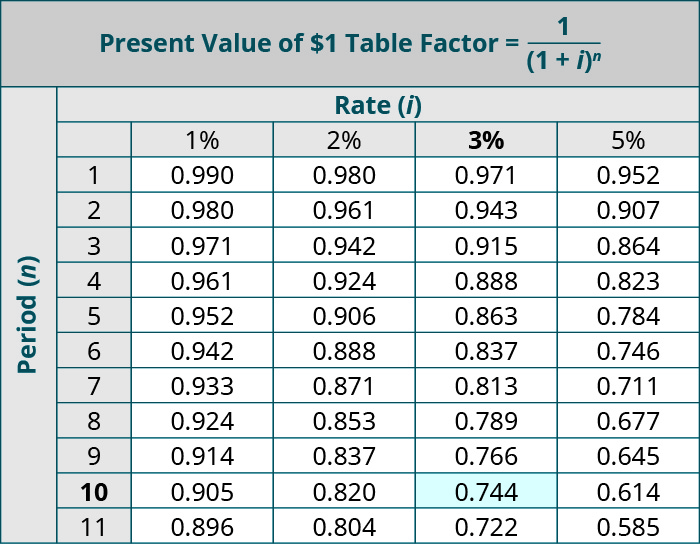
Present Value of $1

When referring to present value, the lump sum return occurs at the end of a period. A business must make up one's mind if this delayed repayment, with interest, is worth the same as, more than than, or less than the initial investment cost. If the deferred payment is more than the initial investment, the company would consider an investment.

To calculate present value of a lump sum, we should use the Present Value of $1 table. For instance, you are interested in saving money for college and want to calculate how much you lot would need put in the bank today to return a sum of $xl,000 in 10 years. The bank returns an involvement rate of 3% per year during these 10 years. Looking at the PV table, northward = 10 years and i = 3% returns a nowadays value cistron of 0.744. Multiplying this factor by the return amount of $twoscore,000 produces $29,760. This means you would need to put in the bank now approximately $29,760 to take $40,000 in x years.

As mentioned, to determine the nowadays value or hereafter value of greenbacks flows, a fiscal calculator, a program such equally Excel, knowledge of the advisable formulas, or a gear up of tables must be used. Though we illustrate examples in the text using tables, nosotros recognize the value of these other adding instruments and have included affiliate assessments that use multiple approaches to determining present and future value. Knowledge of unlike approaches to determining nowadays and future value is useful as at that place are situations, such as having fractional interest rates, 8.45% for example, in which a financial calculator or a programme such as Excel would be needed to accurately determine present or future value.

Annuity Tabular array

As discussed previously, annuities are a serial of equal payments made over fourth dimension, and ordinary annuities pay the equal installment at the terminate of each payment period inside the series. This tin can aid a concern understand how their periodic returns translate into today'south value.

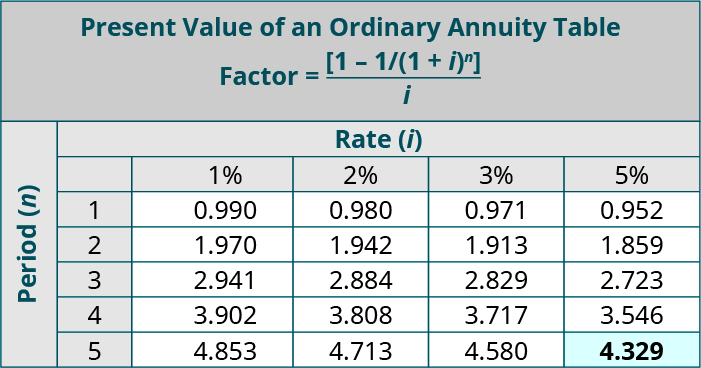
For instance, assume that Sam needs to borrow money for college and anticipates that she will be able to repay the loan in $i,200 annual payments for each of 5 years. If the lender charges v% per year for similar loans, how much cash would the banking company be willing to lend Sam today? In this case, she would employ the Present Value of an Ordinary Annuity table in Appendix B, where n = five and i = 5%. This yields a present value factor of 4.329. The current value of the cash menstruation each period is calculated as four.329 × $1,200 = $five,194.fourscore. Therefore, Sam could borrow $five,194.80 now given the repayment parameters.

Our focus has been on examples of ordinary annuities (annuities due and other more complicated annuity examples are addressed in advanced accounting courses). With annuities due, the cash flow occurs at the showtime of the catamenia. For instance, if you wanted to deposit a lump sum of money into an account and make monthly rent payments starting today, the beginning payment would exist made the same mean solar day that you fabricated the deposit into the funding business relationship. Because of this timing deviation in the withdrawals from the annuity due, the procedure of computing annuity due is somewhat unlike from the methods that you've covered for ordinary annuities.

Determining Present Value

Determine the present value for each of the following situations. Use the present value tables provided in Appendix B when needed, and round answers to the nearest cent where required.

1. Y'all are saving for higher and you want to render a sum of $100,000 in 12 years. The banking company returns an interest charge per unit of 5% after these 12 years.
2. You need to borrow coin for higher and tin can afford a yearly payment to the lending institution of $1,000 per yr for the next 8 years. The involvement rate charged past the lending institution is 3% per year.

Solution

a. Utilize PV of $1 table. Present value gene where n = 12 and i = v is 0.557. 0.557 × $100,000 = $55,700. b. Use PV of an ordinary annuity table. Nowadays value factor where n = 8 and i = 3 is 7.020. seven.020 × $1,000 = $7,020.

For a lucky few, winning the lottery can exist a dream come true and the option to take a one-time payout or receive payments over several years does not seem to affair at the fourth dimension. This lottery payout calculator shows how fourth dimension value of money may affect your have-abode winnings.

Fundamental Concepts and Summary

• A dollar is worth more today than it will exist in the future. This is due to many reasons including the ability of investment in today'due south economy, marketplace aggrandizement, and the ability to use the money in the present to make more money in the futurity, with interest.
• Present value expresses the hereafter value of a dollar in today's (nowadays) value. Present value tables, showing the present value factor intersection of periods and interest rate, are used to multiply by the final payout amount to compute today's value.
• The futurity value shows what the value of an investment will be afterwards a sure menstruum of time. Time to come value tables, showing the future value factor intersection of periods and interest rate, are used to multiply past the initial investment amount to compute time to come value.
• A lump sum is a ane-fourth dimension payment after a certain period of time, whereas an ordinary annuity involves equal installments in a series of payments over time. A business tin use lump sum or ordinary annuity calculations for present value and future value calculations.

(Figure)Y'all are explaining fourth dimension value of money factors to your friend. Which factor would yous explain every bit existence larger?

1. The futurity value of $ane for 12 periods at 6% is larger.
2. The present value of $1 for 12 periods at 6% is larger.
3. Neither one is larger considering they are equal.
4. There is non enough information given to reply this question.

(Figure)If you lot are saving the aforementioned amount each month in order to buy a new sports auto when the new models are released, which of the following will help you determine the savings needed?

1. time to come value of ane dollar ($1)
2. present value of ane dollar ($ane)
3. future value of an ordinary annuity
4. present value of an ordinary annuity

(Figure)You want to invest $8,000 at an annual interest rate of 8% that compounds annually for 12 years. Which table will help y'all make up one's mind the value of your account at the end of 12 years?

1. future value of i dollar ($one)
2. present value of ane dollar ($1)
3. future value of an ordinary annuity
4. present value of an ordinary annuity

(Figure)Using the information provided, what transaction represents the all-time application of the nowadays value of an annuity due of $1?

1. Falcon Products leases an office edifice for 8 years with annual lease payments of $100,000 to be made at the beginning of each year.
2. Compass, Inc., signs a note of $32,000, which requires the company to pay back the principal plus interest in 4 years.
3. Bahwat Company plans to deposit a lump sum of $100,000 for the construction of a solar subcontract in four years.
4. NYC Industries leases a automobile for four yearly almanac lease payments of $12,000, where payments are made at the end of each year.

(Effigy)Grummet Company is acquiring a new woods lathe with a cash purchase toll of $80,000. The Forest Primary Industries (the manufacturer) has agreed to accept $23,500 at the stop of each of the next 4 years. Based on this deal, how much interest volition Grummet pay over the life of the loan?

1. $94,000
2. $80,000
3. $23,500
4. $fourteen,000

(Figure)The process that determines the present value of a single payment or stream of payments to be received is ________.

1. compounding
2. discounting
3. annuity
4. lump-sum

(Figure)The procedure of reinvesting interest earned to generate additional earnings over time is ________.

1. compounding
2. discounting
3. annuity
4. lump-sum

(Figure)What is future value and what is ane example where it might exist used?

(Effigy)Why do businesses consider time value of money earlier making an investment decision?

They need to know what the future value is of their investment compared to today's nowadays value, and what potential earnings they could see because of delayed payment.

(Figure)What determines the anticipated interest rate payout for an investment?

(Effigy)To calculate nowadays value of a lump sum, which table would be used?

The Present Value of $1 tabular array.

(Figure)What is the definition of nowadays value?

(Figure)You put $250 in the bank for 5 years at 12%.

1. If interest is added at the end of the yr, how much will you take in the banking concern afterwards one year? Calculate the amount yous volition accept in the bank at the end of twelvemonth ii and continue to calculate all the style to the stop of the fifth twelvemonth.
2. Utilize the future value of $1 table in Appendix B and verify that your reply is correct.

(Figure)If you invest $12,000 today, how much will you accept in (for further instructions on hereafter value in Excel, come across Appendix C):

1. 10 years at 9%
2. 8 years at 12%
3. 14 years at xv%
4. 19 years at xviii%

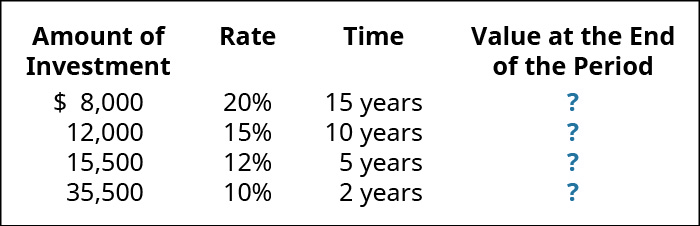
(Figure)You have been depositing money into an account yearly based on the following amounts, rates, and times. What is the value of that investment account at the end of that period?

(Figure)How much would you lot invest today in order to receive $30,000 in each of the following (for further instructions on present value in Excel, see Appendix C):

1. ten years at ix%
2. eight years at 12%
3. xiv years at 15%
4. nineteen years at eighteen%

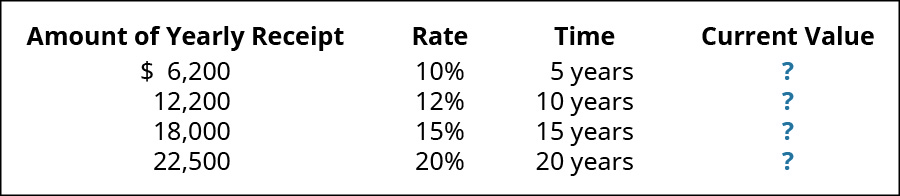
(Effigy)Your friend has a trust fund that volition pay her the following amounts at the given interest charge per unit for the given number of years. Calculate the current (present) value of your friend's trust fund payments. For further instructions on future value in Excel, see Appendix C.

(Figure)Julio Company is considering the purchase of a new bubble packaging machine. If the motorcar volition provide $20,000 annual savings for x years and tin can be sold for $l,000 at the end of the period, what is the nowadays value of the machine investment at a ix% interest rate with savings realized at year terminate?

(Figure)How much must be invested now to receive $30,000 for 10 years if the first $30,000 is received one year from now and the rate is viii%?

(Effigy)You put $600 in the banking company for 3 years at 15%.

1. If interest is added at the finish of the yr, how much will y'all have in the bank later one twelvemonth? Calculate the amount you will have in the banking company at the end of year ii and proceed to summate all the way to the end of the third year.
2. Use the time to come value of $ane tabular array in Appendix B and verify that your answer is correct.

(Figure)If yous invest $xv,000 today, how much will you lot have in (for farther instructions on future value in Excel, see Appendix C):

1. 20 years at 22%
2. 12 years at 10%
3. 5 years at 14%
4. 2 years at seven%

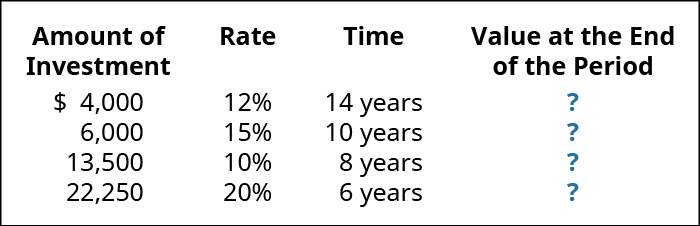
(Figure)You take been depositing money into an account yearly based on the following investment amounts, rates and times. What is the value of that investment account at the end of that menses?

(Figure)How much would you invest today in order to receive $30,000 in each of the following (for further instructions on present value in Excel, come across Appendix C):

1. xx years at 22%
2. 12 years at x%
3. 5 years at 14%
4. ii years at seven%

(Figure)Your friend has a trust fund that volition pay her the following amounts at the given interest rate for the given number of years. Summate the current (present) value of your friend's trust fund payments. For further instructions on nowadays value in Excel, run across Appendix C.

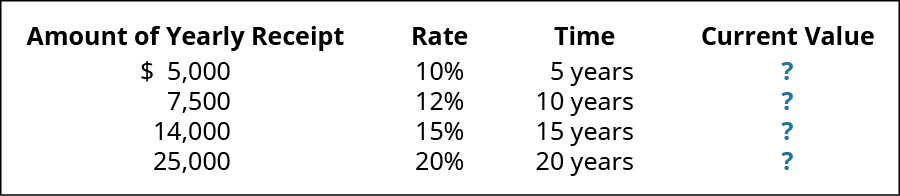
(Figure)Conestoga Plumbing plans to invest in a new pump that is anticipated to provide annual savings for 10 years of $fifty,000. The pump tin exist sold at the terminate of the period for $100,000. What is the present value of the investment in the pump at a 9% interest rate given that savings are realized at year end?

(Figure)How much must be invested now to receive $l,000 for viii years if the starting time $50,000 is received in i year and the charge per unit is 10%?

(Figure)Utilise the tables in Appendix B to answer the post-obit questions.

1. If yous would similar to accumulate $2,500 over the next four years when the interest rate is 15%, how much practise you need to eolith in the account?
2. If you place $6,200 in a savings business relationship, how much volition you have at the finish of 7 years with a 12% interest rate?
3. You invest $8,000 per year for 10 years at 12% involvement, how much will you take at the terminate of 10 years?
4. You lot win the lottery and can either receive $750,000 as a lump sum or $50,000 per year for 20 years. Bold you can earn 8% interest, which practice you recommend and why?

(Figure)Ralston Consulting, Inc., has a $25,000 overdue debt with Supplier No. i. The visitor is low on greenbacks, with only $seven,000 in the checking account and does not want to borrow whatsoever more cash. Supplier No. 1 agrees to settle the account in 1 of 2 ways:

Choice ane: Pay $7,000 at present and $23,750 when some large projects are finished, two years from today.

Option 2: Pay $35,000 three years from today, when fifty-fifty larger projects are finished.

Assuming that the only factor in the decision is the price of coin (8%), which pick should Ralston choose?

(Figure)Utilize the tables in Appendix B to answer the following questions.

1. If you would like to accumulate $iv,200 over the next 6 years when the involvement rate is 8%, how much practise y'all need to deposit in the account?
2. If you place $8,700 in a savings account, how much will y'all have at the terminate of 12 years with an interest rate of viii%?
3. You invest $two,000 per twelvemonth, at the stop of the year, for 20 years at 10% involvement. How much volition y'all take at the end of 20 years?
4. You win the lottery and can either receive $500,000 equally a lump sum or $sixty,000 per year for xx years. Assuming you tin can earn 3% interest, which do you recommend and why?

(Effigy)Chang Consulting, Inc., has a $15,000 overdue debt with Supplier No. ane. The company is low on cash, with merely $4,000 in the checking account and does not want to borrow any more than cash. Supplier No. i agrees to settle the account in ane of two ways:

Selection 1: Pay $four,000 now and $18,750 when some big projects are finished, two years from today.

Pick 2: Pay $25,000 iii years from today, when even larger projects are finished.

Assuming that the only cistron in the determination is the cost of money (eight%), which option should Clary choose?

(Figure)Would you rather have $7,500 today or at the end of 20 years after it has been invested at 15%? Explain your respond.

Glossary

annuity

series of equal payments made over time

annuities due

equal installments paid at the start of each payment period inside the series

compounding

earning involvement on previous interest earned, along with the interest earned on the original investment

discounting

procedure that determines the present value of a single payment or stream of payments to be received

future value (FV)

value of an investment after a certain catamenia of time

lump sum

1-time payment or repayment of funds at a particular signal in time

ordinary annuities

equal installments paid at the stop of each payment catamenia inside the series

present value (PV)

future value of an investment expressed in today'southward value

fourth dimension value of coin

assertion that the value of a dollar today is worth more than than the value of a dollar in the futurity

callihanstor1972.blogspot.com

Source: https://opentextbc.ca/principlesofaccountingv2openstax/chapter/explain-the-time-value-of-money-and-calculate-present-and-future-values-of-lump-sums-and-annuities/

Share this post